在2018年下半年开始接触DOA估计时，拿到程序就对信号产生存在疑问，多方求证思考，2019年得到这份答卷，2022年有了做个人网站（博客）的想法，把此问题整理，发布为本人的第一篇博客。

无论是采用何种阵列、何种算法，经典的干涉仪测向算法也好，子空间类算法、稀疏重构类算法也罢，均匀阵列、稀疏阵列、MIMO等等各种阵列，仿真实验中，信号的产生模块都是相同的，有些时候，相关论文复现结果与论文原作者结果有较大差异，可能就是信号模型和原作者不同造成的。本博客就遇到的几种信号产生方法进行讨论，分析不同产生方法的原理、使用场景和一些小细节。

信号有关基础

按照阵列接受数据模型 X=AS+N ，其中 S 为信号， N 为噪声， X 为接收数据。
为了模拟实际情况，信号、噪声、接收数据通常为复数形式，复信号的频谱为单边带信号，相对于实信号，其有以下优点

避免混叠
节约带宽
不损失能量

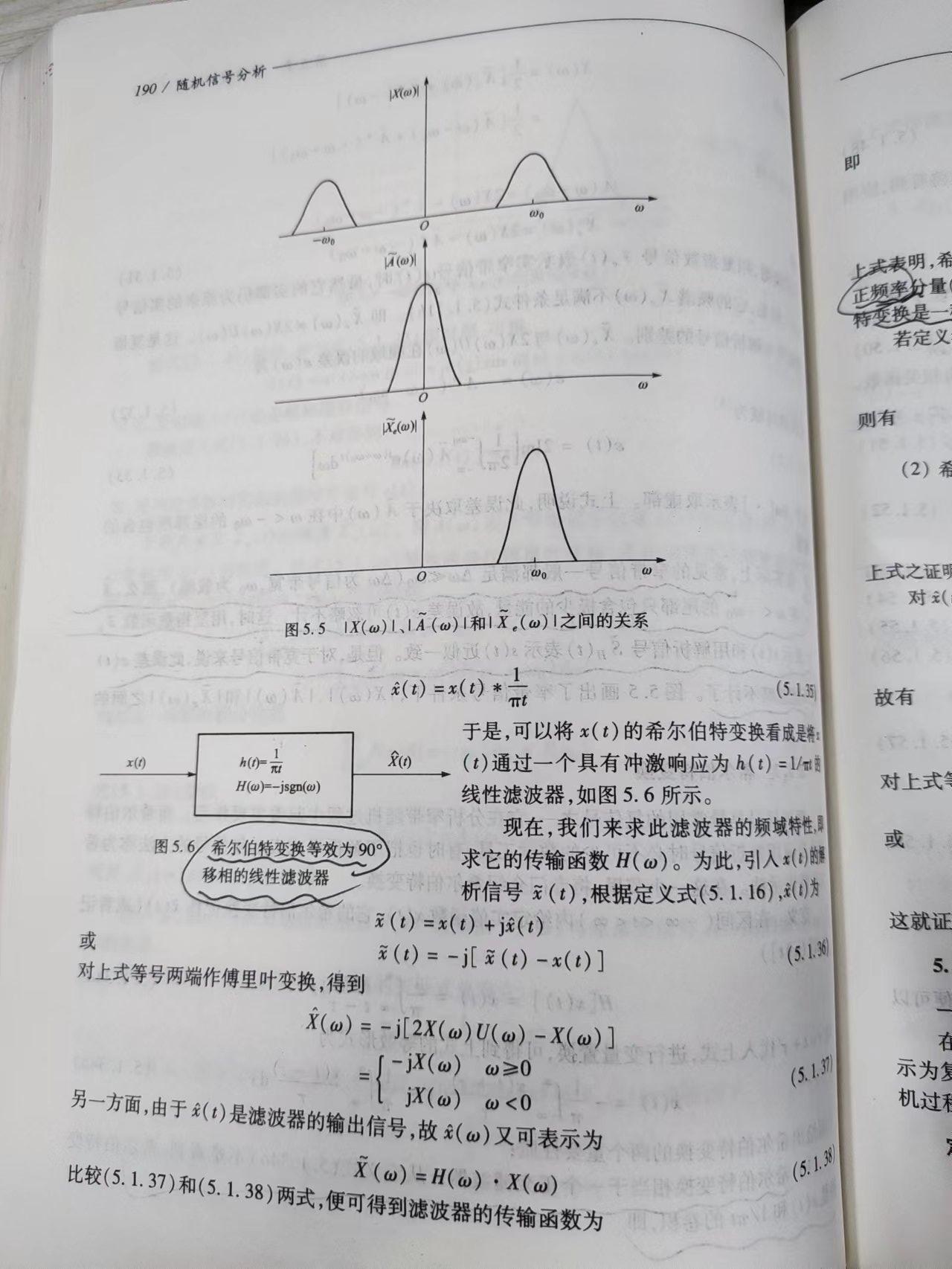
按照窄带随机过程的理论，将实信号变为复信号（解析信号），可通过希尔伯特变换，也可以通过复指数函数的方法。

窄带信号复指数两种表示
窄带信号复指数频谱
希尔伯特变换
希尔伯特变换

信号幅度和相位分布特性

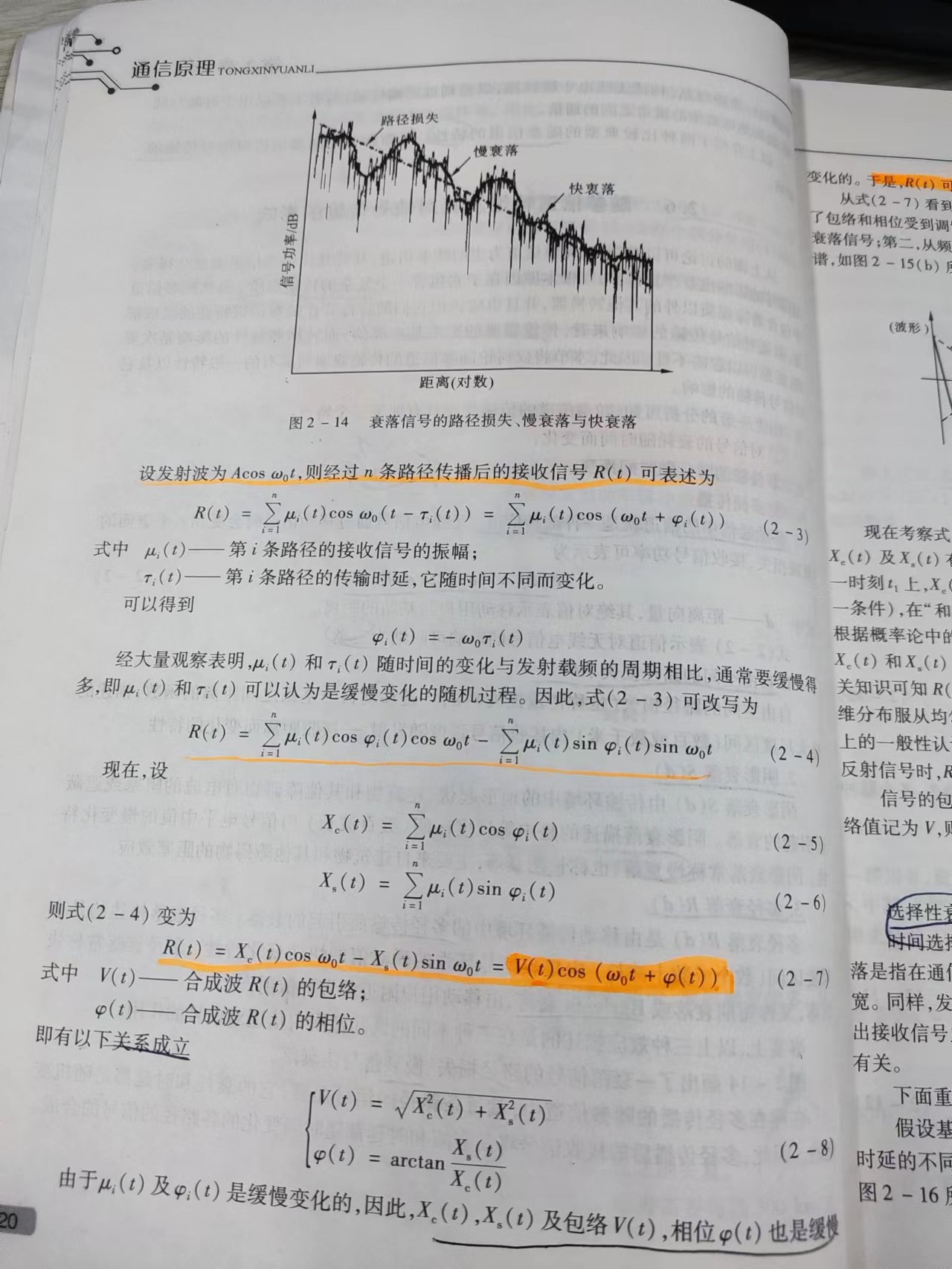
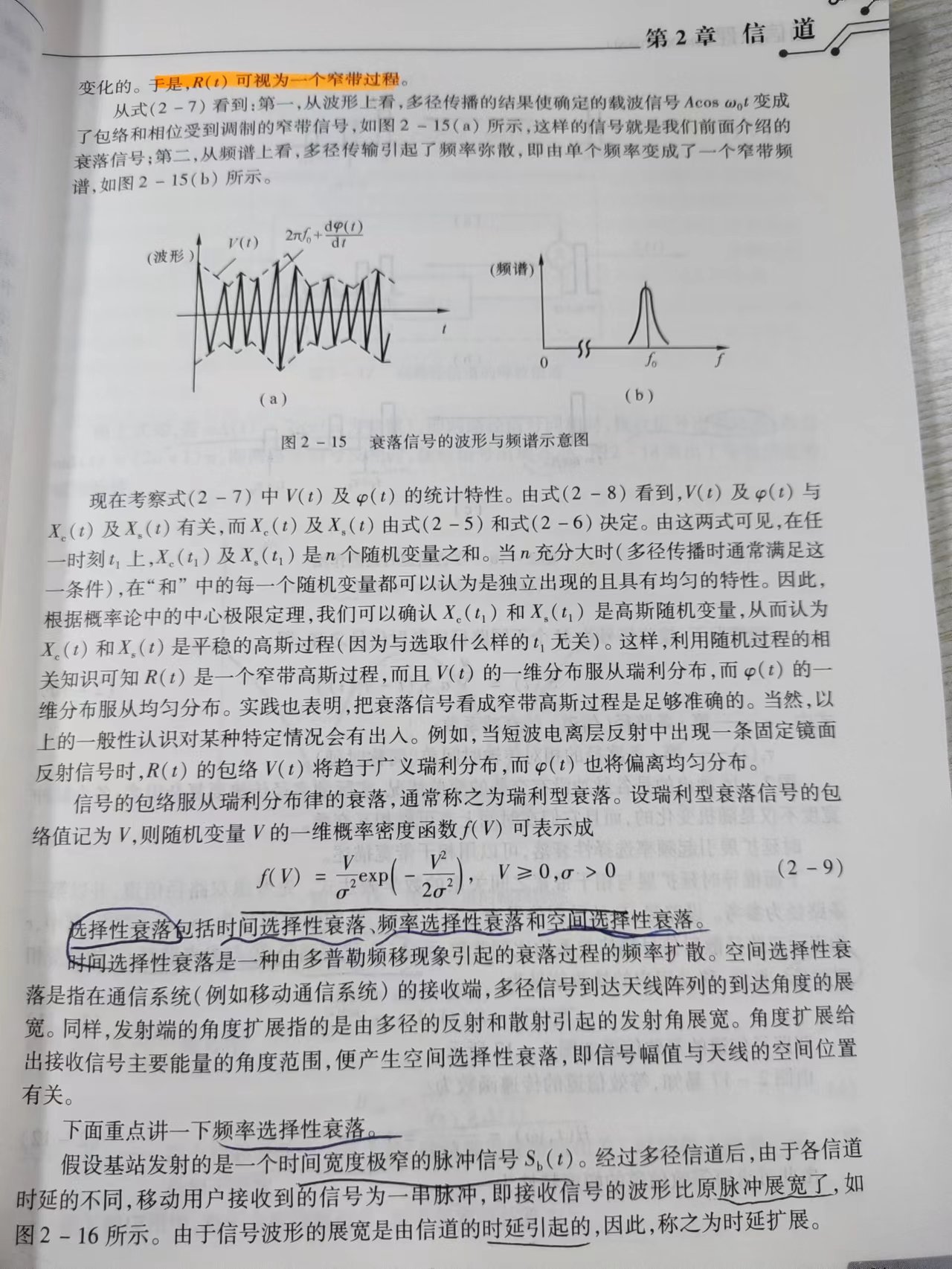
在 通信原理 理论中，信号在发射端到接收端，实际接收到的信号可能是衰落和时延都随时间变化的各路径的信号的合成。经过多径传播等因素影响，从波形上看，载波信号变成了包络和相位受到调制的窄带信号，从频谱上看，其变成了窄带频谱，即窄带随机过程。
多径衰落后的幅度和相位公式
考察其幅度相位统计特性，当多径传播的路径充分大，其 幅度服从瑞利分布，相位一般服从均匀分布
多径衰落后的幅度和相位分布

何为瑞利分布

当一个随机二维向量的两个分量呈独立的、有着相同的方差的正态分布时，这个向量的模呈瑞利分布。瑞利分布是最常见的用于描述平坦衰落信号接收包络或独立多径分量接受包络统计时变特性的一种分布类型。两个正交高斯噪声信号之和的包络服从瑞利分布。通信中很多信道的噪声满足这种分布。
瑞利分布的模的平方服从指数分布。
在通信系统中，随机接收信号的幅度通常用瑞利分布描述。
服从复高斯分布的变量的模用瑞丽分布描述。

瑞利分布程序

clear all;close all;
sigma=2; % 瑞利分布参数sigma
fs=1e7; % 采样率，单位：Hz
t=1e-3; % 随机序列长度，单位：s
t1=0:1/fs:t-1/fs;
n=length(t1);
rand(‘state’,0); % 把均匀分布伪随机发生器置为0状态
u=rand(1,n); % 产生（0-1）单位均匀信号
x=sqrt(2*log2(1./u))*sigma; % 广义均匀分布与单位均匀分布之间的关系
subplot(211);plot(x); % 输出信号图
xlabel(‘t(单位:s)’);
title(‘瑞利分布信号’); % 输出信号的直方图
subplot(212);hist(x,0:0.2:20);
title(‘瑞利分布信号直方图’);
来源：张德丰编著 《MATLAB数字信号处理与应用》 北京:清华大学出版社,2010
链接：https://blog.csdn.net/u013346007/article/details/54310953

  • 瑞丽分布产生方式2
    瑞丽分布产生2
    如图所示，产生的是正态分布的信号，根据 何为瑞利分布 所示，一个随机二维向量的两个分量呈独立的、有着相同的方差的正态分布时，这个向量的模呈瑞利分布，信号的实部如图7所示，虚部的模如图7所示，相位相差90°，其实部、虚部的模就是瑞利分布，如程序所示。

信号产生部分程序

首先给出噪声部分程序 

1
2
3
4
5
6
7
8
9
for m=1:sensorNum
    for n=1:snapshots
        p3=rand(1,1);
        p4=rand(1,1);
        wr(m,n)=sqrt(-2*log(p3))*cos(2*pi*p4);
        wi(m,n)=sqrt(-2*log(p3))*sin(2*pi*p4);
        NoiseMatrix(m,n)=wr(m,n)+1j*wi(m,n);
    end
end

信号的程序在噪声幅度上加上信噪比 

1
2
3
4
5
6
7
8
9
for m=1:1  %注意此处m仅到1
    for n=1:snapshots
        p1=rand(1,1);
        p2=rand(1,1);
        sr(m,n)=snr*sqrt(-2*log(p1))*cos(2*pi*p2);
        si(m,n)=snr*sqrt(-2*log(p1))*sin(2*pi*p2);
        SourceMatrix(m,n)=sr(m,n)+1j*si(m,n);   %signal
    end
end

产生方法2

上述给出了如何产生瑞丽分布的程序，理论中貌似是对的，但实际中，果真如此吗？这是值得商榷的事情
不难发现，在一众广为流传的程序中，还存在这样的信号产生方式

A=[exp(-j*(0:M-1)d2pisin(doa(1)pi/180)/l);exp(-j(0:M-1)d2pisin(doa(2)pi/180)/l)].’;%阵列流型
t=(0:N-1)Ts;
s1=sqrt(10.^(snr/10))exp(j(2pif0t+pi/1));
s2=sqrt(10.^(snr/10))exp(j(2pif0t+pi/2));
s=[s1;s2];%仿真信号,显然这是一个相干信源
%x=awgn(s,snr);
x=As+(1/sqrt(2))(randn(M,N)+j*randn(M,N));%加了高斯白噪声后的阵列接收信号
不难发现，这是通过复指数函数的方式产生的复信号，其幅度是稳定的，相位服从均匀分布。

  • 思考，为什么这样产生信号呢？

信号幅度稳定的原因

在上文讨论信号包络为瑞丽分布的时候，信号的频率为高频，经过多径传播，接收到的信号包络为瑞利分布，其描述的是在小尺度区间（几个波长到几十个波长）内接收信号幅度瞬时值的快速变化特性，实际进行采样时，通常会进行下变频，然后带通采样，这时，DOA估计使用的数据已经不是到达接收天线时的原始数据了，进行下变频后，信号包络变得平坦，考虑到前端的处理，此时信号幅度就采用的常信号的方式。

产生方法3

方法3与方法2类似，结合方法1和方法2，信号的幅度稳定，相位随机，可以产生一组独立信号。

总结

两种信号产生方式均合理，一种考虑的时天线接收到的模拟数据，一种考虑的是实际下变频后采样的数字信号，不同的场景下，有不同的信号产生方式，需要根据实际需要进行改变。

参考文献

《通信原理》哈尔滨工程大学出版社，张晓林、宁晓燕，2017版
《随机信号分析》北京理工大学出版社，朱华
《深入浅出通信原理》

后记

在做DOA估计之初（2018年下半年），就曾经思考过程序这样写的原因，当时问实验室多位师兄，王jianing师兄告诉我，他拿到这个程序也曾问过上面师兄师姐这个问题，未果，经过他的思考，第一种信号产生方式，p1到p4采用随机数是为了产生独立信号，现在再次思索，相位部分p2随机，即可产生独立信号，幅度部分的p1随机就未免没有意义了。
pengzhanli师兄告诉我，采用复信号的原因是为了降低带宽，会有好处，也符合实际应用场景中的IQ数据，但未解决为什么幅度这样做。
实验室也曾有师妹仿真文章，采用第一种信号产生方式，得不到想象中的结果，和原作者结果差异很大，多次查看程序，后发现，原作者采用实际中模型，信号幅度稳定，相位连续。
这个问题虽然很简单，我们做研究一般是针对算法的本体，很少对算法之前的工作进行研究思考，导致在细节上出错，因此记录下此博客，以此为戒，为后续其他人遇到相同的问题提供参考。